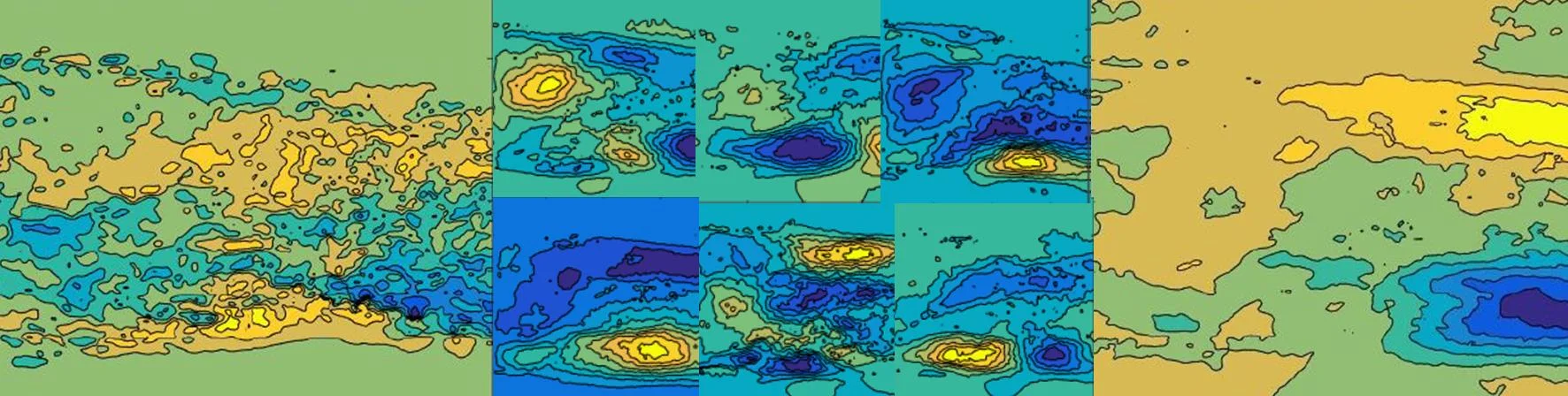
Data-Driven Modelling

Upon simulating or experimentally interrogating a fluid flow, one typically obtains data sets of very high dimension.  To make sense of such data, modal decomposition algorithms attempt to extract coherent structures which are of importance to the dynamics of the flow. The Dynamic Mode Decomposition (DMD) algorithm is the perhaps the most widely known method of this type, and we work on developing new "optimal" versions of it - the Optimal Mode Decomposition (OMD) algorithm - in addition to investigating the theoretical backing for such approaches. 

Dynamic Modes of high Reynolds number flow past an axisymmetric bluff body.

Dynamic Modes of high Reynolds number flow past an axisymmetric bluff body.

Related Publications

  • Beit-Sadi M, Wynn A, Krol J, Data Driven Feature Identification and Sparse Representation of Turbulent Flows, 2019, 11th International Symposium on Turbulence and Shear Flow Phenomena.

  • Krol J, Wynn A, 2017, Dynamic reconstruction and data reconstruction for subsampled or irregularly sampled data, Journal of Fluid Mechancs, 825, 133-166. Link.

  • Wynn A., Pearson D.S., Ganapathisubramani B., Goulart P.J., 2013, Optimal mode decomposition for unsteady flows, Journal of Fluid Mechanics, 733, 473-503. Link. 

  • Goulart P.J., Wynn A., Pearson D., 2012, Optimal mode decomposition for high dimensional systems, 51st IEEE Conference on Decision and Control, Pages: 4965-4970. Link. 

Associated Group Members